Home
Data Science
Linear Regression

How to optimize Linear Regression using Gradient Descent?

Gradient Descent is a commonly used algorithm for finding parameters that minimize the cost function.

What is Linear Regression?

Linear Regression is one of the easiest, most efficient, moreover, a popular machine learning algorithm that comes under supervised learning performs regression tasks to predict results. Regression analysis is a statistical approach to understanding the relationship between two or more variables like how one changes according to the other. The basic idea is to find the regression line that fits best for the data given.
 

The line can be represented by the slope-intercept formula: y = mx + b where x, y, m, and b are the independent variable, dependent variable, slope, and y-intercept respectively.

In machine learning it can be written as:  y(pred) = θ1 + θ2.x (hypothesis function) Finding  θ2 and θ1 will satisfy the equation and will give us the y-predictions.

Cost Function for Linear Regression:

What is Gradient Descent?

Is there any way to optimize your machine learning model to yield maximum performance? Let's say if you are building a model that can predict the stock prices for you, It's always better to know all the possible ways to optimize your model performance so that you can have more benefits. Strategies like Grid Search may help to increase the accuracy of the model by tuning the hyperparameters. Another way to optimize models like Linear Regression is by Gradient Descent. Before we dive into the concepts of gradient descent it's good to understand it simply. Gradient Descent is a commonly used algorithm for finding parameters that minimize the cost function. This is an iterative process where the cost decreases on each iteration until we achieve the optimal solution. The primary goal is to reach the minimum value along the curve that minimizes the cost function.  There are three main Gradient Descent algorithms, they are Batch Gradient Descent, Stochastic Gradient Descent, and Mini-Batch Gradient Descent depending on the structure and amount of data.

Gradient Descent

In Gradient Descent there are three main hyperparameters, One is the learning rate or learning step as shown in the picture, the number of iterations, and the initial random value. We set an initial random value and the learning rate determines at which rate does it want to move. If the learning rate is too low it takes a lot of time to iterate through all the values thus increasing the time complexity. Meanwhile, if the learning rate is too high, it may skip the global or local minimum failing to find the optimal solution. So the learning rate must be set between these two. At the time when the algorithm reaches the bottom of the curve or minimum value, we'll get the values of coefficients that have the minimum cost.

Linear Regression using Gradient Descent

Now you have some idea about Linear Regression and Gradient Descent, Let's plug them together in order to check how Gradient Descent can be used to optimize Linear Regression. 

The Mean Squared Error is the cost function here. So let's substitute the slope-intercept formula to the Mean Squared Error function and we'll get:
 
substituting the value of ȳ

Take the partial derivative with respect to m:

Derivative with respect to m, MSE(cost function)
Derivative with respect to m

Now let's take the partial derivative with respect to b:

Derivative with respect to b, MSE(cost function)

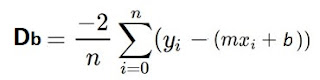Derivative with respect to b

Update the value for m and b in each iteration:

m(current) = m - learning rate * Dm
b(current) = b - learning rate * Db

we'll repeat this step until we reach the minimum value that is zero. If the minimum value is zero then the model has 100% accuracy. 

Implementing the model

import numpy as np
import matplotlib.pyplot as plt

def Gradient_Descent(X,y):
    m = b = 0
    iteration = 1000
    learning_rate = 0.001
    n = len(X)
    
    
    for i in range(iteration):
        y_pred = m * X + b # slope intercept formula
        cost = (1/n)*sum([val**2 for val in (y-y_pred)]) # Cost function
        
        # partial derivative with respect to m
        md = -(2/n) * sum(X*(y - y_pred)) 

        # partial derivative with respect to b
        bd = -(2/n) * sum(y - y_pred)

        # updating m and b values
        m = m - learning_rate * md
        b = b - learning_rate * bd
        
    print("M:{}, B:{}, iter:{}, cost:{} pred:{}".format(m,b,i,cost, y_pred))
    
    # plotting the regression line formed
    plt.scatter(X, y) 
    plt.plot([min(X), max(X)], [min(y_pred), max(y_pred)], color='red')
    plt.show()
    

X = np.array([[3],[2],[4],[5],[9],[6],[2],[8]])
y = np.array([[5],[5],[7],[10],[16],[12],[3],[14]])


Gradient_Descent(X,y)

If you run this code, you'll find the value of m and b are updating frequently in each iteration, thus the cost begins to shrink down resulting more accurate prediction. You can also set the learning rate and iterations to different values depending upon the data you are provided.

Regression line