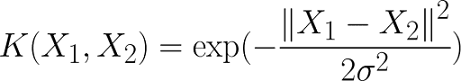Introduction
The Radial Basis Function (RBF) kernel is one of the most powerful, useful, and popular kernels in the Support Vector Machine (SVM) family of classifiers. In this article, we’ll discuss what exactly makes this kernel so powerful, look at its working, and study examples of it in action. We’ll also provide code samples for implementing the RBF kernel from scratch in Python that illustrates how to use the RBF kernel on your own data sets. Let’s dive in!...
What are Kernels in SVM?
SVM is an algorithm that has shown great success in the field of classification. It separates the data into different categories by finding the best hyperplane and maximizing the distance between points. To this end, a kernel function will be introduced to demonstrate how it works with support vector machines. Kernel functions are a very powerful tool for exploring high-dimensional spaces. They allow us to do linear discriminants on nonlinear manifolds, which can lead to higher accuracies and robustness than traditional linear models alone.
If you want to have a quick overview of SVM kernels, check this article: SVM Kernels: Polynomial Kernel - From Scratch Using Python.
The kernel function is just a mathematical function that converts a low-dimensional input space into a higher-dimensional space. This is done by mapping the data into a new feature space. In this space, the data will be linearly separable. This means that a support vector machine can be used to find a hyperplane that separates the data.
For example, if the input 𝑥 is two-dimensional, the kernel function will map it into a three-dimensional space. In this space, the data will be linearly separable.
In addition, they provide more features than those of other algorithms such as neural networks or tree ensembles in some kinds of problems involving handwritten recognition, face detection, etc because they extract intrinsic properties of data points through a kernel function.
The RBF Kernel
RBF short for Radial Basis Function Kernel is a very powerful kernel used in SVM. Unlike linear or polynomial kernels, RBF is more complex and efficient at the same time that it can combine multiple polynomial kernels multiple times of different degrees to project the non-linearly separable data into higher dimensional space so that it can be separable using a hyperplane.
The RBF kernel works by mapping the data into a high-dimensional space by finding the dot products and squares of all the features in the dataset and then performing the classification using the basic idea of Linear SVM. For projecting the data into a higher dimensional space, the RBF kernel uses the so-called radial basis function which can be written as:
Here ||X1 - X2||^2 is known as the Squared Euclidean Distance and σ is a free parameter that can be used to tune the equation.
When introducing a new parameter ℽ = 1 / 2σ^2, the equation will be
The equation is really simple here, the
Squared Euclidean Distance is multiplied by the
gamma parameter and then finding the
exponent of the whole. This equation can find the
transformed inner products for mapping the data into higher dimensions
directly without actually transforming the entire dataset which leads to inefficiency. And this is why it is known as the RBF kernel
function.
The distribution graph of RBF Kernel will look like this:
As you can see that the Distribution graph of the RBF kernel actually looks like the Gaussian Distribution curve which is known as a bell-shaped curve. Thus RBF kernel is also known as Gaussian Radial Basis Kernel.
RBF kernel is most popularly used with K-Nearest Neighbors and Support Vector Machines.
Implementing RBF kernel with SVM using Python
Now let's see the RBF kernel in action! For that, we need a dataset that is non-linearly separable which can be created using the Scikit-Learn make_circles dataset.
Creating the dataset
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import make_circles
X, y = make_circles(n_samples=500, noise=0.06, random_state=42)
df = pd.DataFrame(dict(x1=X[:, 0], x2=X[:, 1], y=y))
Now let's plot the dataset to see its distribution.
colors = {0:'blue', 1:'yellow'}
fig, ax = plt.subplots()
grouped = df.groupby('y')
for key, group in grouped:
group.plot(ax=ax, kind='scatter', x='x1', y='x2', label=key, color = colors[key])
plt.show()
Now let's try the fit this data to a Linear SVM to check the accuracy of predictions.
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score
clf = SVC(kernel="linear")
clf.fit(X, y)
pred = clf.predict(X)
print("Accuracy: ",accuracy_score(pred, y))
------
Accuracy: 0.496
When fitting the data into a Linear SVM model, the accuracy is around 50% which is quite low. Now let's see if we can solve this a little bit using Polynomial Kernel.
clf = SVC(kernel="poly")
clf.fit(X, y)
pred = clf.predict(X)
print("Accuracy: ",accuracy_score(pred, y))
-------
Accuracy: 0.566
Well, the accuracy of the model has increased to 57% by using a polynomial kernel. However, this result is not bad but not a satisfying accuracy for a machine learning model. Now let's try to do the same using RBF kernel.
The RBF kernel using Python
Let's create a function in python for performing RBF kernel.
def RBF(X, gamma):
# Free parameter gamma
if gamma == None:
gamma = 1.0/X.shape[1]
# RBF kernel Equation
K = np.exp(-gamma * np.sum((X - X[:,np.newaxis])**2, axis = -1))
return K
This function accepts two parameters, one is the dataset for sure, and another is the gamma parameter. The gamma parameter can be any value that tunes the equation. You can try giving different values to gamma to see the change in the accuracy of prediction.
Now let's transform the dataset using the following RBF kernel,
Let's see how much accuracy we reached using RBF,
clf = SVC(kernel="linear")
clf.fit(X, y)
pred = clf.predict(X)
print("Accuracy: ",accuracy_score(pred, y))
----
Accuracy: 0.94
That's great! The accuracy of the model is now 94% when using the RBF kernel for this particular dataset. This happens because the RBF kernel can transform the data points as much as possible for fitting the hyperplane between those two classes of data points. This makes the RBF kernel so powerful when comes to kernelized models.
RBF kernel can be able to solve most of the overlapped datasets (just like above). However, you don't need to think that RBF kernel can be used to solve almost any given dataset of different distributions. In some cases, the RBF kernel will not be good for some kinds of datasets, so there we can try other kernel functions.


.png)