Implementing SVM from Scratch Using Python

Introduction

In this guide, we’re going to implement the linear support vector machine algorithm from scratch in Python. Our goal will be to minimize the cost function, which we’ll use to train our model, and maximize the margin, which we’ll use to predict values against new, untrained data. We’ll be using NumPy — one of Python’s most popular machine learning libraries — to handle all of our calculations, so you won’t need any additional software or libraries installed on your computer to follow along! If you want to have a quick overview of the basics of SVM and its calculations check this article: Primal Formulation of SVM: A Simplified Guide | Machine Learning.

The main goal of SVM

We looked at the working of SVM in detail in previous articles, but to give a quick understanding of the goal of SVM let's explain it! The main goal of SVM is the maximization of margins between two different classes. That means that you want to make sure that as many points in one class are on one side of the decision boundary and as many points in the other class are on the other side. 

When this happens, all points with a higher degree of separation will be correctly classified while all points with a lower degree of separation will be misclassified.

SVM Diagram

So when the marginal distance between these two classes is at their maximum, they become the optimal solution for maximizing margin and minimizing risk. As such, it becomes a lot easier to classify new points without any error because they can just be placed on either side of the decision boundary based on which class it belongs to. If there are errors though then there's always something called regularization which allows us to penalize models so that they generalize better for new data points.

The equation for Soft Margin SVM

The regularization term for SVM will look like this:

This term is known as the regularizer which we need to use for maximizing the margin and minimizing the loss. 

When adding two terminologies for our gradient descent to work, ie, the number of errors in training(C), and the sum of the value of error(𝚺𝛇) the equation can be written as:

This particular error term added allows some classification errors to occur for avoiding overfitting of our model, ie, the hyperplane will not be changed if there are small errors in classification. This model is known as a Soft Margin SVM.

Now let's rewrite this equation in the form of a Loss function view. The Loss function we are using here is known as the Hinge Loss function which would look like this:

Let's rewrite the optimization term, including the Hinge Loss function:

This is the term we need to optimize using our gradient descent algorithm in order to obtain parameters w(weights) and b(bias)

Implementing SVM from scratch in python

Writing the SVM class

# svm.py

import numpy as np

class SVM:
    def __init__(self, C = 1.0):
        # C = error term
        self.C = C
        self.w = 0
        self.b = 0

First, we created a class SVM and initialized some values. The C term is known as the error term which we need to add for optimizing the function

Hinge Loss calculation

    # Hinge Loss Function / Calculation
    def hingeloss(self, w, b, x, y):
        # Regularizer term
        reg = 0.5 * (w * w)
        for i in range(x.shape[0]):
            # Optimization term
            opt_term = y[i] * ((np.dot(w, x[i])) + b)
            # calculating loss
            loss = reg + self.C * max(0, 1-opt_term)
        return loss[0][0]

Let's understand what's happening here. First, we are calculating the value of the regularizer term and assign it to variable reg. Then iterating over the number of samples and calculating the loss using the optimization function.

Gradient Descent optimization

Now let's create the gradient descent function inside the fit method in order to get the best parameters w and b. 

    def fit(self, X, Y, batch_size=100, learning_rate=0.001, epochs=1000):
        # The number of features in X
        number_of_features = X.shape[1]
        # The number of Samples in X
        number_of_samples = X.shape[0]
        c = self.C
        # Creating ids from 0 to number_of_samples - 1
        ids = np.arange(number_of_samples)
        # Shuffling the samples randomly
        np.random.shuffle(ids)
        # creating an array of zeros
        w = np.zeros((1, number_of_features))
        b = 0
        losses = []
        # Gradient Descent logic
        for i in range(epochs):
            # Calculating the Hinge Loss
            l = self.hingeloss(w, b, X, Y)
            # Appending all losses 
            losses.append(l)
            
            # Starting from 0 to the number of samples with batch_size as interval
            for batch_initial in range(0, number_of_samples, batch_size):
                gradw = 0
                gradb = 0
                for j in range(batch_initial, batch_initial + batch_size):
                    if j < number_of_samples:
                        x = ids[j]
                        ti = Y[x] * (np.dot(w, X[x].T) + b)
                        if ti > 1:
                            gradw += 0
                            gradb += 0
                        else:
                            # Calculating the gradients
                            #w.r.t w 
                            gradw += c * Y[x] * X[x]
                            # w.r.t b
                            gradb += c * Y[x]
                # Updating weights and bias
                w = w - learning_rate * w + learning_rate * gradw
                b = b + learning_rate * gradb
        
        self.w = w
        self.b = b
        return self.w, self.b, losses  

What happens in this fit method is really simple, we are trying to reduce the loss in consecutive iterations and find the best parameters w and b. Note that here we are using Batch Gradient Descent. The weights(w) and bias(b) are updated in every iteration using the gradients and the learning rate resulting in the minimization of the loss. When the optimal parameters are found the method simply returns it along with the losses.

Predict Method

    def predict(self, X):
        
        prediction = np.dot(X, self.w[0]) + self.b # w.x + b
        return np.sign(prediction)

Performing Classification

Alright, we have created an SVM class only with the help of NumPy. Now let's do some classification to see our model in action. 

Creating random dataset

# prediction.py

from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from svm import SVM
# Creating dataset
X, y = datasets.make_blobs(
        n_samples = 100, # Number of samples
        n_features = 2, # Features
        centers = 2,
        cluster_std = 1,
        random_state=40
    )
# Classes 1 and -1
y = np.where(y == 0, -1, 1)

Splitting the dataset

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=42)

Training the SVM model

svm = SVM()
w, b, losses = svm.fit(X_train, y_train)

Making predictions and testing accuracy

prediction = svm.predict(X_test)
# Loss value
lss = losses.pop()
print("Loss:", lss)
print("Prediction:", prediction)
print("Accuracy:", accuracy_score(prediction, y_test))
print("w, b:", [w, b])

----

Loss: 0.0991126738798482
Prediction: [-1.  1. -1. -1.  1.  1.  1.  1. -1.  1. -1. -1.  1.  1. -1. -1.  1. -1.
  1. -1.  1.  1. -1.  1.  1.  1. -1. -1. -1. -1.  1. -1. -1.  1.  1. -1.
  1. -1. -1.  1.  1.  1.  1.  1.  1. -1.  1.  1.  1.  1.]
Accuracy: 1.0
w, b: [array([[0.44477983, 0.15109913]]), 0.05700000000000004]

Visualizing SVM

Visualizing SVM is one of the best ways to find how it is being fitted to the training data. We can do this using the matplotlib package.

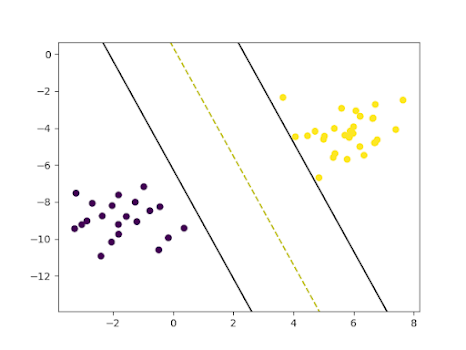
# Visualizing the scatter plot of the dataset
def visualize_dataset():
    plt.scatter(X[:, 0], X[:, 1], c=y)

# Visualizing SVM
def visualize_svm():
    def get_hyperplane_value(x, w, b, offset):
        return (-w[0][0] * x + b + offset) / w[0][1]
    fig = plt.figure()
    ax = fig.add_subplot(1,1,1)
    plt.scatter(X_test[:, 0], X_test[:, 1], marker="o", c=y_test)
    x0_1 = np.amin(X_test[:, 0])
    x0_2 = np.amax(X_test[:, 0])
    x1_1 = get_hyperplane_value(x0_1, w, b, 0)
    x1_2 = get_hyperplane_value(x0_2, w, b, 0)
    x1_1_m = get_hyperplane_value(x0_1, w, b, -1)
    x1_2_m = get_hyperplane_value(x0_2, w, b, -1)
    x1_1_p = get_hyperplane_value(x0_1, w, b, 1)
    x1_2_p = get_hyperplane_value(x0_2, w, b, 1)
    ax.plot([x0_1, x0_2], [x1_1, x1_2], "y--")
    ax.plot([x0_1, x0_2], [x1_1_m, x1_2_m], "k")
    ax.plot([x0_1, x0_2], [x1_1_p, x1_2_p], "k")
    x1_min = np.amin(X[:, 1])
    x1_max = np.amax(X[:, 1])
    ax.set_ylim([x1_min - 3, x1_max + 3])
    plt.show()

visualize_dataset()
visualize_svm()

Visualization of dataset

Visualization of SVM on the test set

Complete version of SVM algorithm

import numpy as np

class SVM:
    def __init__(self, C = 1.0):
        # C = error term
        self.C = C
        self.w = 0
        self.b = 0
    # Hinge Loss Function / Calculation
    def hingeloss(self, w, b, x, y):
        # Regularizer term
        reg = 0.5 * (w * w)
        for i in range(x.shape[0]):
            # Optimization term
            opt_term = y[i] * ((np.dot(w, x[i])) + b)
            # calculating loss
            loss = reg + self.C * max(0, 1-opt_term)
        return loss[0][0]
    def fit(self, X, Y, batch_size=100, learning_rate=0.001, epochs=1000):
        # The number of features in X
        number_of_features = X.shape[1]
        # The number of Samples in X
        number_of_samples = X.shape[0]
        c = self.C
        # Creating ids from 0 to number_of_samples - 1
        ids = np.arange(number_of_samples)
        # Shuffling the samples randomly
        np.random.shuffle(ids)
        # creating an array of zeros
        w = np.zeros((1, number_of_features))
        b = 0
        losses = []
        # Gradient Descent logic
        for i in range(epochs):
            # Calculating the Hinge Loss
            l = self.hingeloss(w, b, X, Y)
            # Appending all losses 
            losses.append(l)
            
            # Starting from 0 to the number of samples with batch_size as interval
            for batch_initial in range(0, number_of_samples, batch_size):
                gradw = 0
                gradb = 0
                for j in range(batch_initial, batch_initial+ batch_size):
                    if j < number_of_samples:
                        x = ids[j]
                        ti = Y[x] * (np.dot(w, X[x].T) + b)
                        if ti > 1:
                            gradw += 0
                            gradb += 0
                        else:
                            # Calculating the gradients
                            #w.r.t w 
                            gradw += c * Y[x] * X[x]
                            # w.r.t b
                            gradb += c * Y[x]
                # Updating weights and bias
                w = w - learning_rate * w + learning_rate * gradw
                b = b + learning_rate * gradb
        
        self.w = w
        self.b = b
        return self.w, self.b, losses
    def predict(self, X):
        
        prediction = np.dot(X, self.w[0]) + self.b # w.x + b
        return np.sign(prediction)
    

Thanks for reading!

Must-read Articles: A Detailed Overview to the Basics of Support Vector Machines in Machine Learning

Primal Formulation of SVM: A Simplified Guide | Machine Learning