 |
Introduction
The correlation coefficient measures the strength and direction of a linear relationship between two variables. This coefficient can be used to describe both the relationship between two sets of data (sample) or to describe how two sets of data relating to the entire population from which they were selected (population). The formula may be slightly different depending on what you are calculating, but the idea behind each calculation remains the same. Let's understand more about the correlation coefficient in this article.
The meaning of correlation coefficient
Let's understand Correlation simply, it is a measure of how two variables change together. For example, if you are looking at height and weight, the height and weight will be correlated. The correlation coefficient measures how well that relationship is: If height goes up by 1 inch, does weight go up by 1 pound? If height goes up by 10 inches, does weight go up by 10 pounds? And so on. The correlation coefficient can range from -1 to +1; if it's -1 then there is a perfect negative relationship between x and y (if x goes up then y goes down); if it's +1 there is a perfect positive relationship (if x goes up then y goes up).
If you want to get a complete overview of Pearson's Correlation Coefficient check this article: Correlation Coefficient in Machine Learning
Now you have an intuition on what is a correlation, but what are population correlation and sample correlation? Let's see.
What are population and sample in statistics?
The population in statistics is a collection of items that are being studied. It is usually a large group of people or things, but it can also be a small group. A sample is a subset of data taken from a larger population. A statistic is any numerical value that describes or summarizes information about a sample or a population.
Suppose we want to calculate the average height of the population in a country. It's not practical to measure the height of the entire population. So we need to take something known as a sample. We can choose any number of people, as long as they are randomly selected from all over that country. In order for them to be randomly selected, they must not be chosen because they are related or friends with each other. For example, if you choose your best friend and his/her family, then it is not a random sample. After choosing our sample, we need to collect their heights. So, now we have collected data about a sample. This sample can be statistically determined in order to estimate the average heights of the population in that country. So population in statistics is the entire set of things that can be drawn for statistical purposes. In fact, it is not a statistic but a parameter.
 |
| Population and Sample |
Calculation of Sample Correlation Coefficient
How to calculate the Sample Correlation Coefficient? Well, we can say that the sample correlation coefficient of two variables is the sample covariance of two variables divided by the product of the sample standard deviation of two variables. If that doesn't make much sense let's see what the equations should look like:
The equation for Correlation in relation to Covariance and Standard Deviation:
 |
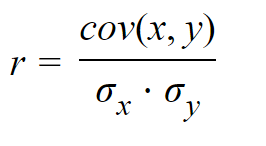| Correlation Coefficient Eqn |
The equation for Sample Covariance:
 |
| Sample Covariance Eqn |
Now for the sample standard deviation, the equation will be:
 |
| Sample Standard Deviation Eqn |
Example for Sample Correlation Coefficient
 |
| Table for Calculation |
Sample Standard Deviation for x:
So we got 0.6863 as our sample correlation coefficient which is approximately 68% and is positive.
Calculation of Population Correlation Coefficient
 |
| Population Covariance Eqn |
Population Standard Deviation of x and y is given by:
 |
| Population Standard Deviation Eqn |
Example for Population Correlation Coefficient
