Introduction
Correlation, standard deviation, variance, and covariance are all used in the math world to describe different elements of the same concept. To understand the relation between correlation, standard deviation, variance, and covariance you must first know what each of these terms means. This article will discuss each of these terms one by one and also the relationship between them.
The meaning of Correlation Coefficient
Correlation is defined as the strength of a linear relationship between two variables. The strength of a correlation can be measured by its correlation coefficient (r). A positive value indicates that two variables move in the same direction (e.g., both increase or both decrease), while a negative value indicates that they move in opposite directions. A perfect positive correlation would have an r-value of 1; if there were no relationship at all, it would have an r-value of 0.
Let's understand Correlation simply, it is a measure of how two variables change together. For example, if you are looking at height and weight, the height and weight will be correlated. The correlation coefficient measures how well that relationship is: If height goes up by 1 inch, does weight go up by 1 pound? If height goes up by 10 inches, does weight go up by 10 pounds? And so on. The correlation coefficient can range from -1 to +1; if it's -1 then there is a perfect negative relationship between x and y (if x goes up then y goes down); if it's +1 there is a perfect positive relationship (if x goes up then y goes up).
If you want to get a complete overview of Pearson's Correlation Coefficient check this article: Correlation Coefficient in Machine Learning
To know how to calculate the population correlation coefficient check this article: How to calculate sample and population correlation coefficient.
What is a variance?
The first term we need to discuss is the variance. The variance of a population is a measure of how far each score in a distribution deviates from its mean. The variance tells us how spread out scores are around their mean value. For example, if you want to calculate how much the height of the population in a country has deviated from its mean value, you can use this statistical measure. The variance is actually defined as the mean squared difference between each data point. This can be understood from the equation.
The equation of variance is given by:
.png "Equation of variance") |
| Equation of variance |
Where S^2 = Variance
xi = The values of observation
x_bar = Mean value of the observation
n = Total number of observation
Let's consider some x and y values:
Our goal is to find the variance of x and y separately, So first we need to find the mean of x values:
Now let's find the Variance of x,
Mean of y values:
The variance of y:
What is a Covariance of two variables?
The equation of covariance is given by:
 |
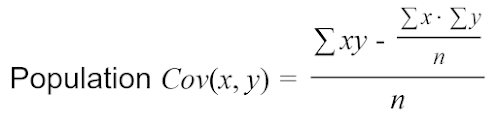| Equation of covariance |
Where x = values regarding x, y = values regarding y, n = Total number of values.
Let's calculate the covariance of x, y
Substituting values from the table to the equation:
The population covariance of the given dataset is 31.5
What is Standard Deviation?
Relation between Covariance, Standard Deviation, and Correlation
So how are these terms related to correlation? For that, let's see the equation of correlation r: |
| Equation of correlation |
From the equation, we can clearly understand the relation between correlation, covariance, and standard deviation. The correlation coefficient(r) is equal to the covariance of the two values divided by the product of its standard deviations.